spiegato semplice
Il problema dei tre corpi non è solo il titolo di una collana di libri prima e di una serie tv ora, ma è una delle questioni più intricate ed affascinanti della fisica e dell'astronomia passata e contemporanea.
La formulazione del problema è apparentemente molto semplice: data la posizione iniziale, la massa e la velocità di tre corpi celesti, è possibile descrivere l’evoluzione delle loro rispettive orbite nel tempo?
Ma nel vasto teatro dello spazio profondo, dove le forze gravitazionali intrecciano i destini dei pianeti, niente è così “semplice” come appare.
Il motivo di questa accelerazione/decelerazione è che i due corpi sono soggetti all'influsso della reciproca attrazione gravitazionale, che agisce in maniera proporzionale rispetto alla loro massa e alla loro distanza, come scoperto da Isaac Newton nella sua legge di gravitazione universale.
Quando il pianeta si allontana dal Sole, la forza gravitazionale diminuisce e l'accelerazione diminuisce di conseguenza.
Questa è la principale dinamica di base del movimento dei corpi celesti nello spazio e solo questo ci basta per iniziare a complicare un po’ le cose e ad entrare nel vivo del famoso problema. In fin dei conti, l’evoluzione di un sistema Terra-Sole, data la poca mobilità di quest’ultimo, può essere visto come un “problema ad 1 solo corpo”.
Questi, come visto nell'esempio precedente, si attraggono e si respingono a vicenda a causa della gravità.
Si può calcolare l'evoluzione futura di un sistema così composto? La risposta è si, e farlo significa scrivere una serie di equazioni differenziali capaci di descrivere il moto futuro dei due corpi a partire dalle loro posizioni e velocità. Queste equazioni, che apparentemente sono anche piuttosto complesse, risultano però tutto sommato risolvibili in forma chiusa e pienamente comprensibili dagli addetti ai lavori.
Ma se complichiamo il sistema aggiungendo solo un'ulteriore corpo celeste, i calcoli sballano improvvisamente. Questo è lo scenario del famoso problema dei tre corpi, e per nostra sfortuna da qui in avanti le cose si iniziano a complicare di molto.
Ma non preoccupatevi, facciamo un passo indietro e cerchiamo di andare con ordine.
Per predire la configurazione di un sistema a 3 corpi nel tempo, in maniera del tutto analoga al problema a 2 corpi, dobbiamo immaginare di poter essere in grado di scrivere una formula matematica capace di spiegare il valore della posizione e della quantità di moto dei tre corpi in ogni istante di tempo.
Idealmente questa formula dovrebbe funzionare per tutte le possibili configurazioni di partenza dei tre corpi e deve poter essere risolta con un numero finito di operazioni matematiche.
Guardiamo quindi da vicino il sistema e proviamo a descrivere cosa succede.
Conoscendo ora qualche rudimento del movimento dei pianeti sappiamo che i vicini A e B, esercitando la forza gravitazionale, si attraggono a vicenda. Fin qui tutto normale. Siamo nel problema dei 2 corpi, quindi siamo perfettamente in grado di descrivere e di calcolare i loro movimenti nel tempo... se non fosse che C, il più lontano dei tre, attrae sia A che B. Quindi bisognerà rifare tutti i calcoli per questo motivo.
Però anche A esercita una forza su C e questo cambia le cose, quindi riaggiustiamo i calcoli. Un momento… anche B spinge su C, quindi dobbiamo ricalcolare di nuovo.
Ma non finisce qui. La nuova configurazione influisce nel modo in cui C attrae A e B, che a sua volta cambia il modo in cui A tira su B e C che cambia il modo in cui B esercita l'attrazione gravitazionale su A e C. Il tutto mentre tutti e tre avanzano lungo la loro rispettiva orbita. In pratica dobbiamo ricalcolare di nuovo, ancora e ancora...
Insomma, come avete capito, l'aumentare anche solo di un singolo grado di libertà nel sistema, provoca un aumento esponenziale di configurazioni possibili, al punto che diventa praticamente impossibile risolvere in forma chiusa uno stato a 3 corpi a causa della complessità matematica che si origina.
Per capire meglio questa complessità, immaginate un sistema a due corpi come il lancio di una moneta. Ci sono solo due risultati possibili: testa o croce. L'analogo del sistema a 3 corpi potrebbe essere quello di lanciare tre dadi. Ci sono 6 possibili esiti per ogni dado ed il numero totale di combinazioni sono 216. Una bella differenza vero?
Ovviamente sia il problema dei due corpi che quello dei tre corpi rappresentano delle situazioni ipotetiche, fatte per comprendere i principi della meccanica orbitale e sono solo dei punti di partenza per molti calcoli nell'esplorazione spaziale e nella dinamica dei satelliti.
Nella realtà esistono interazioni gravitazionali da parte di tanti diversi corpi celesti ben più complesse di quelle descritte, al punto che si arriva a parlare del problema degli n-corpi. Non vi sorprenderà che questi sistemi vengono inquadrati all'interno di quella che si definisce “teoria del caos”.
Se non c'è modo di prevedere i movimenti di questo sistema allora come fa la NASA ad esempio a fare previsioni sulle comete o a calcolare le traiettorie dei satelliti che manda in orbita. In fin dei conti, non sono anche quelli parte del problema dei 3 o più corpi?
In effetti è così, ed una possibile soluzione al caos esiste. Ma per capirla dobbiamo abbandonare il reame della matematica analitica ed abbracciare il mondo dell'integrazione numerica e della probabilità, accettando la possibilità di commettere degli errori.
Il processo utilizzato per predire le orbite di un sistema caotico è basato sulle capacità delle unità di calcolo moderno di simulare la realtà tenendo conto di tutti i vincoli assegnati. Una volta definiti i parametri di simulazione infatti, siamo in grado di generare piccoli segmenti finiti di orbite approssimate di un sistema a 3 corpi.






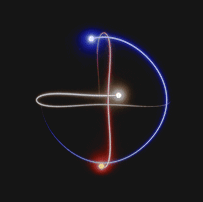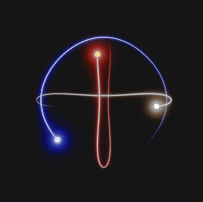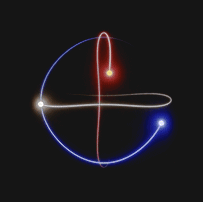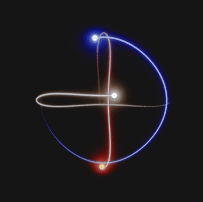













Le soluzioni approssimate vengono calcolate ad ogni istante di tempo. Per ogni istante di tempo infatti, esiste un valore numerico associato alla posizione e alla quantità di moto, che viene utilizzato per calcolare la soluzione al passo temporale successivo.
L'approccio simulativo-statistico è uno strumento essenziale per la pianificazione delle missioni spaziali. Anche se la risposta al problema non potrà mai essere precisa, può essere molto accurata, soprattutto se estendiamo di molto il tempo di esecuzione. Almeno finché la forza bruta delle nostre CPU riesce a resistere. Ma avere una soluzione strutturalmente "imprecisa" ad un sistema già così incredibilmente instabile può portare un qualche tipo di conseguenza catastrofica?
Difficile dare una risposta a questa domanda, ma ci sono almeno due situazioni che potrebbero risentire in maniera negativa di questo errore di approssimazione.
…A meno che un pianeta che prima seguiva un'orbita stabile, decida improvvisamente di cambiare la propria traiettoria facendo sballare le nostre previsioni, con il rischio di gettare la Terra in quella che sarebbe una vera e propria Era del Caos.
Detto questo, probabilmente non c'è da preoccuparsi. In fin dei conti il problema dei tre corpi dietro alla sua apparente semplicità, ci dà modo di riflettere sui nostri limiti e di apprezzare la complessità della natura dell’universo, ricordandoci che tutto sommato, citando il best seller di Liu Cixin, siamo quasi come degli insetti, che osservano inermi e affascinati lo spettacolare volteggio dei corpi celesti sopra le loro teste.
Complimenti
Sei arrivato alla fine dell’articolo in






Danilo Fiumi
26/12/2023


Danilo Fiumi
20/11/2023


Danilo Fiumi
31/07/2023

